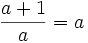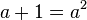Número de Oro
miércoles, 2 de mayo de 2012
Vídeos
Los dos vídeos los hemos visto en clase.
Definición del número de oro

El número áureo es el valor numérico de la proporción que guardan entre sí dos segmentos de recta a y b que cumplen la siguiente relación:
El segmento menor es b. El cociente a / b es el valor del número áureo: φ.
 Surge al plantear el problema geométrico siguiente: partir un segmento en otros dos, de forma que, al dividir la longitud total entre el mayor, obtengamos el mismo resultado que al dividir la longitud del mayor entre la del menor.
Surge al plantear el problema geométrico siguiente: partir un segmento en otros dos, de forma que, al dividir la longitud total entre el mayor, obtengamos el mismo resultado que al dividir la longitud del mayor entre la del menor.Cálculo del valor del número áureo
Dos números a y b están en proporción áurea si se cumple:
Si al número menor (b) le asignamos el valor 1, la igualdad será:
multiplicando ambos miembros por a, obtenemos:
reordenamos:
La solución positiva de la ecuación de segundo grado es:

- que es el valor del número áureo, equivalente a la relación a / b.
 este es el número de oro con más números que arriba.
este es el número de oro con más números que arriba.
Propiedades algebraicas
- Las potencias del número áureo pueden expresarse en función de una suma de potencias de grados inferiores del mismo número, establecida una verdadera sucesión recurrente de potencias.
El caso más simple es:  , cualquiera sea n un número entero. Este caso es una sucesión recurrente de orden k = 2, pues se recurre a dos potencias anteriores.
Una ecuación recurrente de orden k tiene la forma
, cualquiera sea n un número entero. Este caso es una sucesión recurrente de orden k = 2, pues se recurre a dos potencias anteriores.
Una ecuación recurrente de orden k tiene la forma  , donde
, donde  es cualquier número real o complejo y k es un número natural menor o igual a n y mayor o igual a 1. En el caso anterior es
es cualquier número real o complejo y k es un número natural menor o igual a n y mayor o igual a 1. En el caso anterior es  ,
,  y
y  .
En resumen: cualquier potencia del número áureo puede ser considerada como el elemento de una sucesión recurrente de órdenes 2, 4, 6, 8,..., 2k; donde k es un número natural. En la fórmula recurrente es posible que aparezcan potencias negativas de
.
En resumen: cualquier potencia del número áureo puede ser considerada como el elemento de una sucesión recurrente de órdenes 2, 4, 6, 8,..., 2k; donde k es un número natural. En la fórmula recurrente es posible que aparezcan potencias negativas de  , hecho totalmente correcto. Además, una potencia negativa de
, hecho totalmente correcto. Además, una potencia negativa de  corresponde a una potencia positiva de su inverso, la sección áurea.
corresponde a una potencia positiva de su inverso, la sección áurea.
 , cualquiera sea n un número entero. Este caso es una sucesión recurrente de orden k = 2, pues se recurre a dos potencias anteriores.
, cualquiera sea n un número entero. Este caso es una sucesión recurrente de orden k = 2, pues se recurre a dos potencias anteriores. , donde
, donde  es cualquier número real o complejo y k es un número natural menor o igual a n y mayor o igual a 1. En el caso anterior es
es cualquier número real o complejo y k es un número natural menor o igual a n y mayor o igual a 1. En el caso anterior es  ,
,  y
y  .
. , hecho totalmente correcto. Además, una potencia negativa de
, hecho totalmente correcto. Además, una potencia negativa de  corresponde a una potencia positiva de su inverso, la sección áurea.
corresponde a una potencia positiva de su inverso, la sección áurea. El número áureo en la Geometría
El número áureo y la sección áurea están presentes en todos los objetos geométricos regulares o semiregulares en los que haya simetría pentagonal, que sean pentágonos o que aparezca de alguna manera la raíz cuadrada de cinco.
- Relaciones entre las partes del pentágono.
- Relaciones entre las partes del pentágono estrellado, pentáculo o pentagrama.
- Relaciones entre las partes del decágono.
- Relaciones entre las partes del dodecaedro y del icosaedro.
Rectángulo áureo
 Un rectángulo cuyos lados están en una proporción igual a la razón áurea es llamado un rectángulo áureo. Este es un rectángulo muy especial como veremos. Los griegos lo consideraban de particular belleza y lo utilizaron asiduamente en su arquitectura. Al parecer a la mayoría de las personas también les parece más agradable a la vista un rectángulo con esas proporciones entre sus lados, inconscientemente se diseñan infinidad de cosas que resultan tener la forma de un rectángulo áureo: las hojas de papel tamaño carta miden 11 x 8 pulgadas, por ejemplo; esto nos da la proporción 1.37 que se parece a la razón aurea.
Un rectángulo cuyos lados están en una proporción igual a la razón áurea es llamado un rectángulo áureo. Este es un rectángulo muy especial como veremos. Los griegos lo consideraban de particular belleza y lo utilizaron asiduamente en su arquitectura. Al parecer a la mayoría de las personas también les parece más agradable a la vista un rectángulo con esas proporciones entre sus lados, inconscientemente se diseñan infinidad de cosas que resultan tener la forma de un rectángulo áureo: las hojas de papel tamaño carta miden 11 x 8 pulgadas, por ejemplo; esto nos da la proporción 1.37 que se parece a la razón aurea. A partir de él podemos obtener una infinidad de nuevos rectángulos áureos. El proceso es iterativo y consiste en quitar a cada rectángulo áureo un cuadrado, la superficie que queda luego de hacer esto es un nuevo rectángulo áureo.
Suscribirse a:
Entradas (Atom)